【Python】Udemyでデータサイエンスを学ぶ（1）Numpy

Pythonのデータサイエンスの基礎について、Udemyのこちらの学習教材で学んだ内容をまとめています。

【教育・学習】資格・学習

総合情報サイト「コレダ！」がお届けする教育・学習における資格・学習の総合情報サイトです。

環境構築
IPython notebookの使い方
資料
NumPy（ナムパイ）

環境構築

環境構築では、Anacondaというパッケージを利用する。

Anacondaのダウンロードページがこちら

Download Anaconda Distribution | Anaconda

Download Anaconda's open-source Distribution today. Discover the easiest way to perform Python/R data science and machine learning on a single machine.

「Graphical Installer」と「Command Line Installer」がりますが、Graphicalの方がわかりやすいのでGraphicalでインストールします。

インストール方法はこちらを参考（macの場合）

Anaconda（Python3）インストール手順＜macOS用＞

重要PythonにはPyrhon2（2.x系）とPtrhon3（3.x系）の2種類があります。本記事は「Python3」のインストールマニュアルです注意当記事で紹介しているAnacondaは、20

Anacondaとは何か？

データ解析に必要なライブラリをひとまとめにしてくれているもの

IPythonはJupyterという名前に変わっています！

IPython notebookの使い方

以下コマンド実行で、Jupyter のブラウザが開き、ローカルサーバーが立ち上がる。

$ ipython notebook

新規ファイルを作成する

「新規」> 「Python3」

そうするとPythonのコードが入力できる画面が表れる。

コード実行はcontrol + Enter

新しい入力領域の追加

「+」ボタンをクリック

「Shift + Enter」でコード実行と、新規行追加を同時にできる。

ここで書いたコードをそのまま保存できる。

閉じる

ブラウザを閉じるときは、ターミナルで「control + C」

資料

テキストの資料は以下にまとめられている。

Udemy資料

NumPy（ナムパイ）

Numpyの詳細ドキュメントは以下参照

NumPy reference — NumPy v2.1 Manual

Numpyを使うときは、最初の行でimportを記述する。

ここではnpとして使用するため以下のように記述する。

import numpy as np

Arrayを作る

shape

◯行◯列を返す。

dtype

データ型を返す。

zeros, ones

全て0、全て1の配列を返す。

以下の場合、数を5つ指定しているため5個の配列が作られる。

np.zeros(5)

> array([0., 0., 0., 0., 0.])

empty

空の配列が生成される

eye

単位行列が生成される。

以下の場合は5行5列が生成される。

np.eye(5)

> 
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

arange

Numpyの配列を返してくれる。

np.arange(5)

> array([0, 1, 2, 3, 4])

np.arange(最初,最後,飛ばす数)

np.arange(5,50,2)

> array([ 5,  7,  9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37,
       39, 41, 43, 45, 47, 49])

Arrayを使った計算

Array同士の掛け算

arr1 = np.array([[1,2,3,4], [5,6,7,8]])
arr1 * arr1

> 
array([[ 1,  4,  9, 16],
       [25, 36, 49, 64]])

要素同士の掛け算が行われる。

これは、その他の四則演算（+, -, /）も同様

数字を使った計算

1 / arr1

> 
array([[1.        , 0.5       , 0.33333333, 0.25      ],
       [0.2       , 0.16666667, 0.14285714, 0.125     ]])

累乗

3乗してみる

arr1 ** 3

>
array([[  1,   8,  27,  64],
       [125, 216, 343, 512]])

Arrayの添え字

arr = np.arange(最初, 要素数)

arr = np.arange(0,11)
arr

> array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

取り出し

arr[1:5]

> array([1, 2, 3, 4])

index 1から、5の１つ手前までという意味

値の代入

indexの0から4までを100に置き換える

arr[0:5] = 100
arr

> array([100, 100, 100, 100, 100,   5,   6,   7,   8,   9,  10])

全ての要素を表現する

まずは0から6までを取得したものをslice_arrに代入する。

それの全てを99に置き換える。

slice_arr = arr[0:6]
slice_arr[:] = 99
slice_arr

> array([99, 99, 99, 99, 99, 99])

コロン:のみで、全てを取得できる。

この状態でarrを呼び出すと、slice_arr同様に99になっており、共有状態となってしまう。

そこでコピーをして使う。

コピー

arrをコピーして、arr_copyというArrayを作る。

arr_copy = arr.copy()

これだと基をそのままにできる。

多次元配列の取り出し

arr_2d = np.array([[5,10,15], [20,25,30], [35,40,45]])
arr_2d[1]

> array([20, 25, 30])

インデックス1の配列が取り出される。

arr_2d[1][0]

> 20

または、こう書くこともできる。
arr_2d[1,0]

インデックス1の配列の中のインデックス0の要素が取り出される。

行・列を指定して取り出し

array([[ 5, 10, 15],
       [20, 25, 30],
       [35, 40, 45]])

arr_2d[:2,1:]

>
array([[10, 15],
       [25, 30]])

配列2を除き、配列の中の要素1以降を取り出す場合の書き方

行と列の入れ替え

3行3列の二次元の配列を作る

import numpy as np
arr = np.arange(9).reshape((3,3))
arr

> 
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

行と列の入れ替え

.Tとするのみ

arr.T

>
array([[0, 3, 6],
       [1, 4, 7],
       [2, 5, 8]])

または

arr.transpose()

transposeの使い方

引数を取ることができる。

以下の場合、0が行、1が列を意味している。

arr.transpose((0,1))

>
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

これだとなにも変わらない

以下の場合だと変えられる。

arr.transpose((1,0))

>
array([[0, 3, 6],
       [1, 4, 7],
       [2, 5, 8]])

行列の掛け算

dot演算子を使う。

array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

np.dot(arr.T, arr)

>
array([[45, 54, 63],
       [54, 66, 78],
       [63, 78, 93]])

三次元配列を作る

12個の要素。2×2の行列が3個

arr3d = np.arange(12).reshape((3,2,2))
arr3d

>
array([[[ 0,  1],
        [ 2,  3]],

       [[ 4,  5],
        [ 6,  7]],

       [[ 8,  9],
        [10, 11]]])

Arrayと計算のための関数

使用するArray

import numpy as np
arr = np.arange(11)
arr

>
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

平方根の計算

np.sqrt(arr)

>
array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,
       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ,
       3.16227766])

自然対数の底(e)を累乗した値を求める

np.exp(arr)

>
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
       5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
       2.98095799e+03, 8.10308393e+03, 2.20264658e+04])

Array同士の足し算

random

乱数を返す。

randn

正規分布内の数を返す。

add

足し算を行う。

A = np.random.randn(10)
A

>
array([ 0.85776644,  1.47820488,  0.19477171, -0.11697498, -0.2377112 ,
       -1.87246147, -0.55880128, -0.16754371,  0.20127718,  0.47155941])

B = np.random.randn(10)
B

>
array([ 1.17118934,  0.77113758,  0.36431352, -0.03095193,  0.93988834,
        0.0480155 , -0.43915582, -1.69361663, -0.9083344 ,  0.65428161])

np.add(A,B)

>
array([ 2.02895577,  2.24934246,  0.55908523, -0.14792691,  0.70217714,
       -1.82444597, -0.9979571 , -1.86116034, -0.70705723,  1.12584102])

AとB２つの配列を作って、足した。

大きい方の要素を取得する

maximum

np.maximum(A,B)

>
array([ 1.17118934,  1.47820488,  0.36431352, -0.03095193,  0.93988834,
        0.0480155 , -0.43915582, -0.16754371,  0.20127718,  0.65428161])

Arrayを使ったデータ処理

グラフの描画をする

matplotlibを使う

描画するグラフをブラウザの中にそのまま表示する

inlineとする

import numpy as np
import matplotlib.pyplot as　ｐｌｔ
%matplotlib inline

-5から5までの0.01刻みのArrayをpointsという名前で用意する。

points = np.arange(-5, 5, 0.01)

points を実行すると、配列に含まれる大量の要素全てが表示される。

そこでmeshgridという中間を省略してくれるメソッドを使う。

meshgrid

dx, dy = np.meshgrid(points, points)

dx
>
array([[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       ...,
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],
       [-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99]])

dy
>
array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ...,
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

dxは横に、dyは縦に並んでいる。

上記配列が視覚的にわかるよう、matploplibのimshowメソッドを使う。

plt.imshow(dx)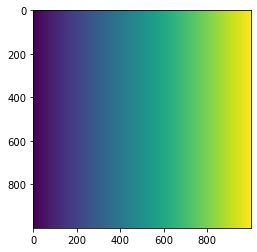

dyも同様に

plt.imshow(dy)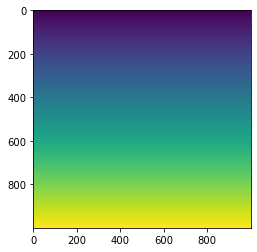

三角関数を使う

z = (np.sin(dx) + np.sin(dy))
z
>
array([[ 1.91784855e+00,  1.92063718e+00,  1.92332964e+00, ...,
        -8.07710558e-03, -5.48108704e-03, -2.78862876e-03],
       [ 1.92063718e+00,  1.92342581e+00,  1.92611827e+00, ...,
        -5.28847682e-03, -2.69245827e-03, -5.85087534e-14],
       [ 1.92332964e+00,  1.92611827e+00,  1.92881072e+00, ...,
        -2.59601854e-03, -5.63993297e-14,  2.69245827e-03],
       ...,
       [-8.07710558e-03, -5.28847682e-03, -2.59601854e-03, ...,
        -1.93400276e+00, -1.93140674e+00, -1.92871428e+00],
       [-5.48108704e-03, -2.69245827e-03, -5.63993297e-14, ...,
        -1.93140674e+00, -1.92881072e+00, -1.92611827e+00],
       [-2.78862876e-03, -5.85087534e-14,  2.69245827e-03, ...,
        -1.92871428e+00, -1.92611827e+00, -1.92342581e+00]])

これを描画すると

plt.imshow(z)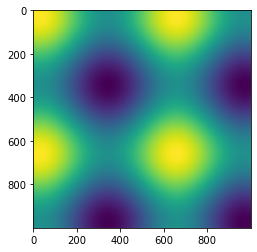

カラーバーを付ける

plt.colorbar()

タイトルを付ける

plt.title('Plot for sin(x)+sin(y)')

これをまとめると

plt.imshow(z)
plt.colorbar()
plt.title('Plot for sin(x)+sin(y)')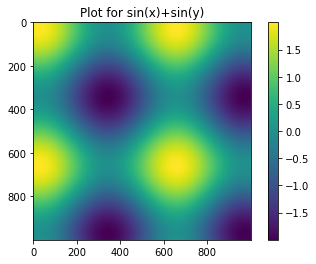

条件式if文

まず2つ数値のArrayと、真偽値のArrayを作る

A = np.array([1,2,3,4])
B = np.array([1000, 2000, 3000, 4000])
condition = np.array([True, True, False, False])

真偽値に応じて、AとBから値を取得し、新しいArrayを作る

リスト内包表記

answer = [(a if cond else b) for a,b,cond in zip (A, B, condition)]
answer

>
[1, 2, 3000, 4000]

(A, B, condition) ここでA, B, conditionをまとめて、新しい配列を作る。

a, bそれぞれにA, Bから、condにはconditionから値が入る。

そして、condがTrueならa、condがFalseならbの配列の値が入る。

条件式where文

answer2 = np.where(condition, A, B)
answer2

>
array([   1,    2, 3000, 4000])

第二引数がTrueだったときに返される値、

第三引数がFalseだったときに返される値

を意味している。

sum

arr = np.array([[1,2,3],[4,5,6],[7,8,9]])
arr

>
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

arr.sum()

> 45

3つの配列を作って、sumで合計を出しました。

全ての要素を足し合わせてくれる。

軸の指定

0行目の合計を出す。

1+4+7で12

arr.sum(0)

> array([12, 15, 18])

mean

平均値を出す。

arr.mean()

> 5.0

std

標準偏差を出す。

arr.std()

> 2.581988897471611

var

分散を出す。

arr.var()

> 6.666666666666667

any

１つでもTrueがあれば全体をTrueとして返す。

bool_arr = np.array([True, False, True])

bool_arr
> array([ True, False,  True])

bool_arr.any()

> True

all

全てがTrueであればTrueを返す。

bool_arr.all()

> False

ソート

ランダムに正規分布の要素を5つ並べたArrayを作り、ソートする。

arr4 = np.random.randn(5)
arr4
> array([ 1.65973474,  0.19125658, -2.56287048, -0.7402054 ,  0.52504004])

arr4.sort()
arr4
> array([-2.56287048, -0.7402054 ,  0.19125658,  0.52504004,  1.65973474])

重複を取り除く

uniqueを使う。

countries = np.array(['Japan', 'USA', 'China', 'Germany', 'Japan', 'USA'])
countries
> array(['Japan', 'USA', 'China', 'Germany', 'Japan', 'USA'], dtype='<U6')

np.unique(countries)
> array(['China', 'Germany', 'Japan', 'USA'], dtype='<U6')

JapanとUSAが重複していたので取り除かれている。

in1d

第一引数の値が、第二引数に入っているかの判定ができる。

np.in1d(['France', 'USA', 'Sweden'], countries)

> array([False,  True, False])

Arrayの入出力

バイナリーデータとして保存

バイナリーデータとはPCに保存できるデータのこと

第一引数にファイル名、第二引数に保存するArrayを記述

np.save('my_array', arr)

読み込み

np.load('my_array.npy')

zip形式で保存

arr1とarr2の2つのファイルをまとめる。

savesとし、拡張子はnpzとするのが一般的。

また、Arrayには、x, yの名前を付ける。

np.savez('ziparrays.npz', x=arr1, y=arr2)
archive_array = np.load('ziparrays.npz')
archive_array

> <numpy.lib.npyio.NpzFile at 0x7ffdd17b28e0>

名前を使ってArrayにアクセスする。

archive_array['x']

> array([0, 1, 2, 3, 4])

テキスト形式で保存

savetxt を使い、第二引数に保存するArrayのarrを指定し、第三引数をdeliniterとし仕切り文字を指定する。

np.savetxt('my_test_text.txt', arr, delimiter=',')

上記ファイルを呼び出す。

!cat my_test_text.txt

以上！環境構築からNumpyについてでした。